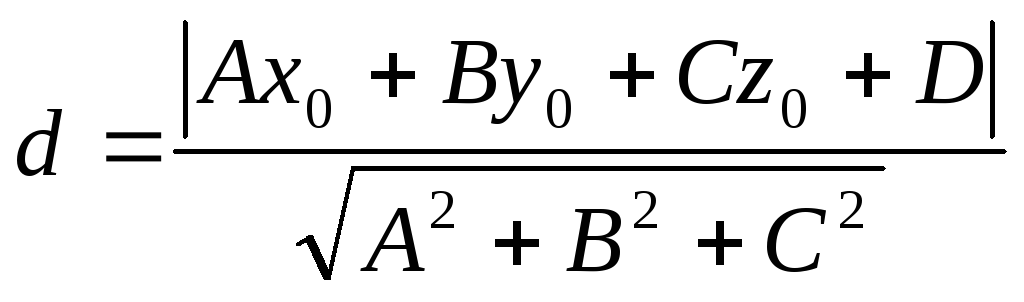Аналитическая геометрия. Часть 2. Аналитическая геометрия в пространстве
В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии в пространстве , которые обычно касаются определения расстояний между объектами, уравнений прямых и плоскостей, углов между прямыми, расстояний между точкой и плоскостью, между прямыми, взаимного расположения прямых и плоскостей в пространстве и т. Решение задачи о пирамиде в аналитической геометрии. Задача 1.








В данном разделе обсуждается понятие векторного иногда его называют линейным пространства. Основные определения были даны в курсе линейной алгебре и здесь мы вкратце повторим их, имея в виду приложения в аналитической геометрии. Это частный случай матриц, так что в качестве операций мы используем матричные операции сложения и умножения на число.

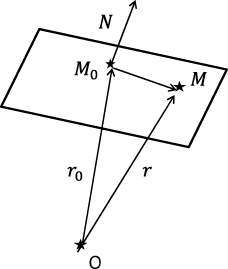



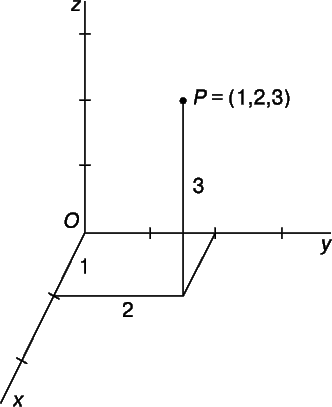





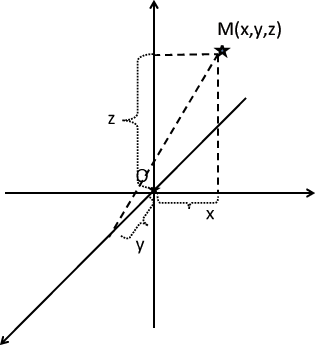
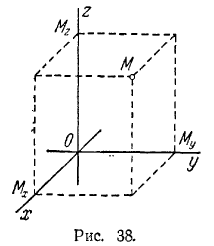
Пусть в пространстве введена прямоугольная система координатOXYZ. Рассмотрим в пространстве некоторую плоскость Q. Поверхности Q соответствует некоторое уравнение. Поверхность, определяемая этим уравнением есть геометрическое место точек в пространстве , координаты которыхx, y, z удовлетворяют этому уравнению. Это означает, что данному уравнению удовлетворяют координаты x, y, z каждой точки, лежащей на поверхности Q, и не удовлетворяют координаты никакой точки, не лежащей на ней. Уравнение называется уравнением данной поверхностиQ.